The process of calling a function by itself is called recursion. Recursion is frequently used in mathematics to solve a complex problem by dividing it into simpler problem of same type. Similarly in programming, it can be used to divide a larger problem many simpler problem and solving them individually. The general format of a recursive function is:
returntype recursive_func ([argument list])
{
statements;
... ... ...
recursive_func ([actual argument])
... ... ...
}
Flowchart for recursion
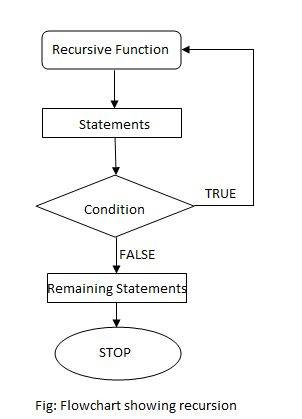
While using recursion, we need to define a proper exit condition to prevent infinite recursive call. Recursion uses a stack to save the content of current function before making a recursive call.
Types of recursion
- Direct Recursion
- Indirect Recursion
Direct Recursion
A function when it calls itself directly is known as Direct Recursion.
For example,
int factorial (int n)
{
if (n==1 || n==0)
return 1;
else
return n*factorial(n-1);
}
Here, inside factorial(int n), it directly calls itself as n*factorial(n-1). This is direct recursion.
Indirect Recursion
A function is said to be indirect recursive if it calls another function and the new function calls the first calling function again.
For example,
int func1(int n)
{
if (n<=1)
return 1;
else
return func2(n);
}
int func2(int n)
{
return func1(n-1);
}
Here, recursion takes place in 2 steps, unlike direct recursion.
- First, func1 calls func2
- Then, func2 calls back the first calling function func1.
Example #1: C++ program print first n fibonacci number using recursion.
#include<iostream>
using namespace std;
int fibo(int num)
{
if(num==1||num==2)
return 1;
else
return (fibo(num-1)+fibo(num-2)); // recursive call
}
int main()
{
int i,n;
cout<<"Enter the required term: ";
cin>>n;
cout<<"First "<<n<<" fibonacci numbers are"<<endl;
for (i=1; i<=n; i++)
cout<<fibo(i)<<endl;
return 0;
}
In this program, concept of recursion is used to generate fibonacci series since a term is represented as the sum of two smaller terms. Fibonacci series is a series where a term is generated by adding two previous term of that series. Mathematically,
tn = tn-1 + tn-2
Here,
- The number of fibonacci terms to be generated is taken from the user and stored in variable n.
- A for loop is used to loop through the number to be generated which is sent to the function fibo. This function is used to calculate and return fibonacci series.
- Inside fibo, if the term-number is 1 or 2, it returns 1. This is because, the first two terms of fibonacci series are both 1. The printed values are 1,1.
- Then the next term-number 3 is passed onto fibo function, since it’s not 1 or 2, the next term in the series is calculated by taking fibo(n – 1) + fibo(n – 2), where n = 3. This calculates the last two terms in the fibonacci series. This is equivalent to fibo(2) + fibo(1), which results in 1 + 1 = 2.
- This recursive loop goes on finally printing the series as 1, 1, 2, 3, 5…
Output
Enter the required term: 7 First 7 fibonacci numbers are 1 1 2 3 5 8 13
Disadvantages of Recursion
- Recursive programs are generally slower than non recursive programs. This is because, recursive function needs to store the previous function call addresses for the correct program jump to take place.
- Requires more memory to hold intermediate states. It is because, recursive program requires the allocation of a new stack frame and each state needs to be placed into the stack frame, unlike non-recursive(iterative) programs.