Recursion in C Programming

The process of calling a function by itself is called recursion and the function which calls itself is called recursive function. Recursion is used to solve various mathematical problems by dividing it into smaller problems. This method of solving a problem is called Divide and Conquer.

In programming, it is used to divide complex problem into simpler ones and solving them individually.

Syntax of Recursive Function

returntype recursive_func ([argument list])
{
    statements;
    ... ... ...
    recursive_func ([actual argument]);
    ... ... ...
}

Flowchart of Recursion

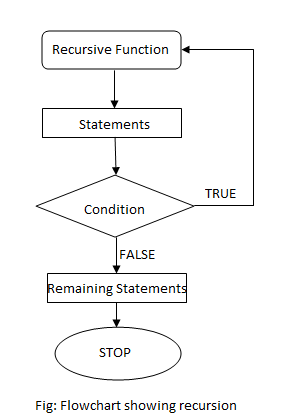
recursion in c programming

Note: In order to prevent infinite recursive call, we need to define proper exit condition in a recursive function.

For example, consider the program below:

Example #1: C Program to show infinite recursive function

#include<stdio.h>

int main()
{
    printf("Hello world");
    main();
    return 0;
}

In this program, we are calling main() from main() which is recursion. But we haven’t defined any condition for the program to exit. Hence this code will print “Hello world” infinitely in the output screen.

Types of recursion

  • Direct Recursion
  • Indirect Recursion

Direct Recursion

A function is said to be direct recursive if it calls itself directly.

Example #2: C Program Function to show direct recursion

int fibo (int n)
{
    if (n==1 || n==2)
        return 1;
    else
        return (fibo(n-1)+fibo(n-2));
}

In this program, fibo() is a direct recursive function. This is because, inside fibo() function, there is a statement which calls fibo() function again directly.

Indirect Recursion

A function is said to be indirect recursive if it calls another function and this new function calls the first calling function again.

Example #3: C Program Function to show indirect recursion

int func1(int n)
{
    if (n<=1)
        return 1;
    else
        return func2(n);
}

int func2(int n)
{
    return func1(n);
}

In this program, func1() calls func2(), which is a new function. But this new function func2() calls the first calling function, func1(), again. This makes the above function an indirect recursive function.

Example #4: C program to calculate factorial of a number using recursion.

#include<stdio.h>
int factorial(int n)
{
    if(n==0)
        return 1;
    else
        return (factorial(n-1)*n);
}

int main()
{
    int num,f;
    printf("Enter a number: ");
    scanf("%d",&num);
    f=factorial(num);
    printf("Factorial of %d = %d",num,f);
    return 0;
}

Here, factorial is calculated using recursion. The formula for calculating factorial of a number n is,

n! = 1*2*...(n-1)*n

Again, we can see

(n-1)! = 1*2*...(n-1)

Hence we can write,

n! = (n-1)! * n

We have implemented this recursive relation in our program.

Here,

  • The number whose factorial is to be found is stored in the variable n.
  • A recursive function factorial(num) calculates the factorial of the number.
  • As factorial is (n-1)! * n, factorial function calculates the factorial by recursively multiplying n with factorial of (n-1).
  • Finally, when n = 0, it returns 1 because 0! = 1.

Output

Enter a number: 7
Factorial of 7 = 5040

Example #5: C program print first n Fibonacci numbers using recursion.

#include<stdio.h>

int fibo(int num)
{
    if(num==1||num==2)
        return 1;
    else
        return (fibo(num-1)+fibo(num-2));  // recursive call
}

int main()
{
    int i,n;
    printf("Enter the required term: ");
    scanf("%d",&n);
    printf("First %d fibonacci numbers aren",n);
    for (i=1; i<=n; i++)
        printf("%dn",fibo(i));
    return 0;
}

This program uses recursion to generate Fibonacci series. In a Fibonacci series, nth term can be obtained by adding (n-1)th and (n-2)th term. Mathematically,

tn = tn-1 + tn-2

Here,

  • The number of fibonacci terms to be generated is taken from the user and stored in variable n.
  • A for loop is used to loop through the number to be generated which is sent to the function fibo. This function is used to calculate and return fibonacci series.
  • Inside fibo, if the term-number is 1 or 2, it returns 1. This is because, the first two terms of fibonacci series are both 1. The printed values are 1,1.
  • Then the next term-number 3 is passed onto fibo function, since it’s not 1 or 2, the next term in the series is calculated by taking fibo(n – 1) + fibo(n – 2), where n = 3. This calculates the last two terms in the fibonacci series. This is equivalent to fibo(2) + fibo(1), which results in 1 + 1 = 2.
  • This recursive loop goes on finally printing the series as 1, 1, 2, 3, 5…

Output

Enter the required term: 7
First 7 fibonacci numbers are
1
1
2
3
5
8
13

Disadvantages of Recursion

  • Recursive programs are generally slower than non recursive programs because it needs to make a function call so the program must save all its current state and retrieve them again later. This consumes more time making recursive programs slower.
  • Recursive programs requires more memory to hold intermediate states in a stack. Non recursive programs don’t have any intermediate states, hence they don’t require any extra memory.